21. Matrix Multiplication
Matrix Multiplication
Now that you've seen how Matrix multiplication is used in state transformation, let's go through some concrete examples, and test your knowledge!
Remember that multiplying two matrices involves a couple steps:
It multiplies each row in the first matrix with the columns in the second, element-wise (that means the number of columns in the first matrix and rows in the second must be equal).
It sums up those multiplied values to form a new value in a new matrix at a specific location.
- ex. If we multiply the first row of the first matrix by the first column of the second, this new, summed value belongs in the first row and first column of the resulting matrix.
- ex. If we multiply the second row of the first matrix by the first column of the second, this new, summed value belongs in the second row and first column of the resulting matrix.
- Matrix multiplication takes practice, so take a look at this page for more examples!
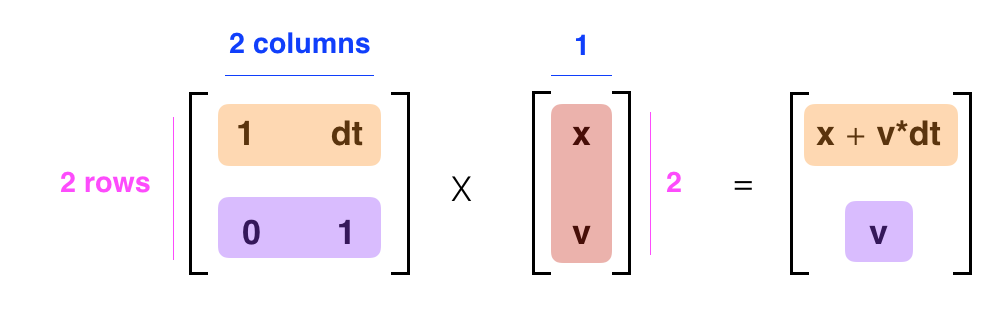
State transformation by matrix multiplication.
Let's consider the case where the position of a self-driving car is at: x = 10 , and velocity,v = 120.
Where would you predict that the car with be in 3 seconds, using matrix multiplication? Well, we'd simply plug in the numbers for x, v, and dt in the transformation equation:
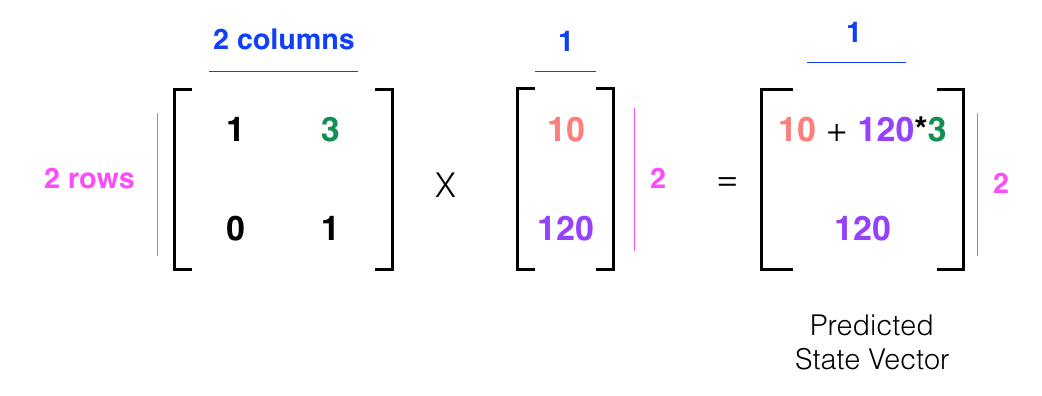
New, predicted state vector.
Predicted State Vector
We'd get a new, predicted state vector with x = 10+120*3. and a constant velocity.
x = 370 and v = 120
Let's try a few more examples.
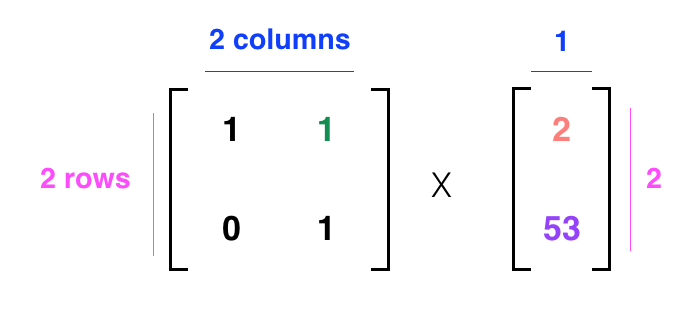
dt = 1, x = 2, and v = 53
SOLUTION:
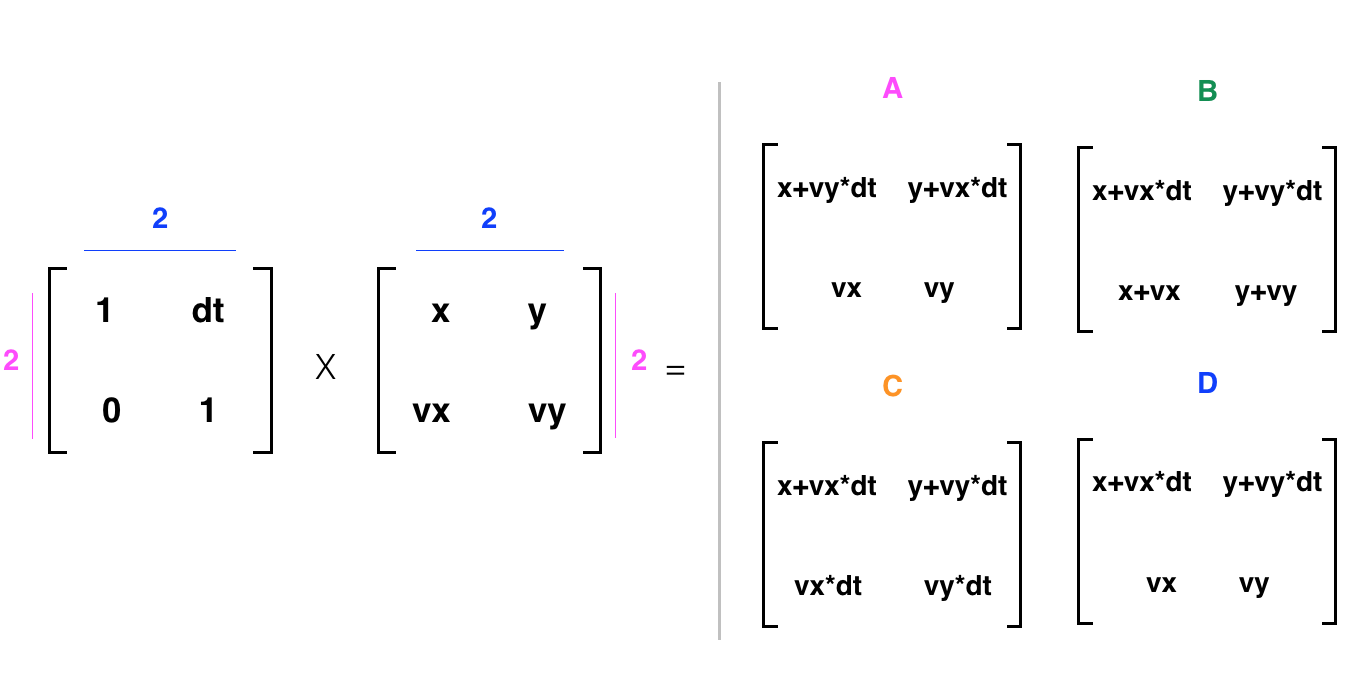
[55, 53]What about for a 2x2 matrix that's not a state vector? Take a look at the scenario below and the options for the resulting matrix.